Speaker
Description
With the increasing communication needs in harsh environment such as underground, submarine or biological tissues where communications methods with radiofrequency (RF) waves are very difficult, the magnetic communication methods, in which the message is transmitted via the magnetic field, are drawing more and more attention. The advantage is the ability of magnetic field to penetrate all non-magnetic materials.
In a magnetic communication system, a sensor is placed in the receiver side to capture the modulated magnetic signal from the transmitter. In a conventional system, the used sensors (coil) are based on the magnet induction principle (Fig.1a) [1]. However, the sensitivity of this type of sensor decreases when the working frequency is relatively low (typically a few tens of kilohertz) and when the size of the coil decreases (in mobile applications). In these conditions, it is relevant to consider other types of magnetic sensors for these communication systems. In this paper, we investigate the possibility of using a Giant Magneto-Impedance (GMI) sensor for magnetic communication (Fig.1b).
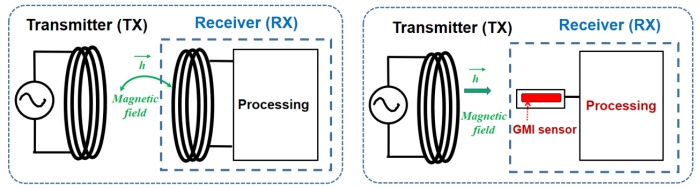
Fig. 1 Communication system with induction-based receiver and GMI based receiver.
The main objective of this work is to compare the sensitivity of this GMI sensor and the conventional coil according to several considerations such as the working frequency and the size of the coil. The underlying idea is to determine the conditions under which the use of the GMI sensor exhibits advantage. This comparison is based on the calculation and the measurement of the intrinsic sensitivities of both sensors.
The sensitivity of a coil is a function of a variety of parameters including its radium $r$, the working frequency $f$ and the number $n$ of turns of the coil, etc. Assuming that the receiving coil is “relatively small”, the sensitivity can be expressed as:
$S_{coil}$=$2nf$$\pi^2$ $r^2$
Meanwhile the sensitivity of a given GMI sensor could be considered as independent of the frequency (until some limit defined by the electronic conditioning and the frequency of the excitation of the GMI element). If we fix two parameters among the three parameters ($n$, $f$, $r$) of the coil, it possible to calculate the upper (or lower) limit for the third parameter beyond which a GMI sensor exhibits better sensitivity. For example, this kind of calculation shows that a coil with $n$ =10 turns and a working frequency $f$ = 60 kHz will be less sensitive than a typical high sensitivity GMI sensor (with sensitivity of about 700 kV/T) when the radius of the coil is smaller than 24 cm.
The equivalent magnetic noise expressed in $T/\sqrt{Hz}$ is another important quantity to be compared. It determines the smallest magnetic field that sensors could measure by multiplying it with the square root of the bandwidth. This smallest field will define the maximum communication range that could be achieved. These comparisons aspects will be detailed in the full paper.
References
[1] J. -Y. Kim, H. J. Lee, J. -H. Lee, J. H. Oh and I. -K. Cho, "Experimental Assessment of a Magnetic Induction-Based Receiver for Magnetic Communication," in IEEE Access, vol. 10, pp. 110076-110087, 2022, doi: 10.1109/ACCESS.2022.3214507.

