Speaker
Description
Physics-Informed Neural Networks (PINNs) are a novel class of neural networks that enable the integration of machine learning and physical laws. This relatively recent algorithmic technology, introduced in 2019, has numerous important scientific applications in engineering sciences, such as real-time simulation, digital twins, inverse computation, and finite element methods.
In this work, we have investigated the contribution of PINNs to 1D/2D magnetic source localization and compared their performance to our classical approaches [3]. Numerical simulation/modeling is not always the optimal solution for physics problems, especially when real-time response is required, simulations are computationally expensive, learning data is available, some parameters of the physical model are unknown or inaccessible for modeling, or when Model Order Reduction (MOR) is needed to develop/implement a multi-physics numerical twin.
Based on this observation, we have studied the performance of PINNs on our 1D/2D benchmark setup and evaluated how it can improve results or accelerate computation times, making it more feasible to apply to scenarios with many sensing elements having complex spatial geometric configurations. Figure 1 compares our classical method [3] with a PINN approach. The relevant parameter is the position error of the magnetic dipole location versus the distance to two sensors, $d$, the sensor noise (defined with $SNR_{m}$ cf. [3]), and a discrepancy in sensor sensitivity.
The main results demonstrate the efficiency of PINNs in modeling the physical system based on a reasonable training dataset. Furthermore, once trained, PINNs surpass the classical method based on minimization functions [3] in terms of computation time, making them a promising approach for real-time applications.
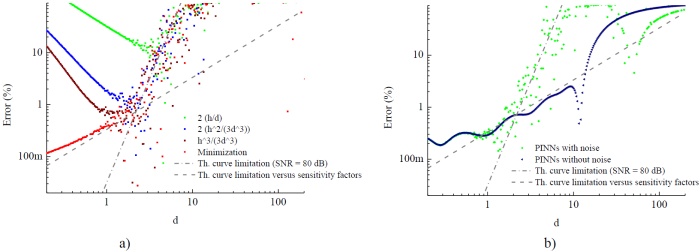
Fig. 1 a) Error in the evaluation of the distance, d, of magnetic dipole to the head of detection based on previous modeling [3], b) errors obtain with PINNs. Both $SNR_{m}$ is 80dB. The PINNs $d$ training range (Log scale - 5 million samples) is given from 0.1 to 10 and the magnetization amplitude, $\mu$, varies from (0.3, 1, 3).
References
[1] M. Raissi, P. Perdikaris, and G. E. Karniadakis, “Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations,” Journal of Computational Physics, vol. 378. Elsevier BV, pp. 686–707, Feb. 2019. doi: 10.1016/j.jcp.2018.10.045.
[2] S. Besnard, F. Jurie, and J. Fadili, “Simpinns: Simulation-Driven Physics-Informed Neural Networks for Enhanced Performance in Nonlinear Inverse Problems,” 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, Oct. 31, 2023. doi: 10.1109/whispers61460.2023.10430751.
[3] C. Dolabdjian and C. Cordier, “Analysis by Systemic Approach of Magnetic Dipole Source Location Performances by Using an IoT Software Gradiometer Head,” IEEE Sensors Journal, vol. 22, no. 8. Institute of Electrical and Electronics Engineers (IEEE), pp. 7709–7716, Apr. 15, 2022. doi: 10.1109/jsen.2022.3156858.

