Speaker
Description
An energy harvester is a device that converts ambient energy from various sources such as light, vibration, or heat into electrical energy for powering electronic devices in situations where it is not practical to rely on conventional power sources, such as batteries or connections to the electrical grid. There are different types of energy harvesters, each designed to take advantage of specific energy sources, such as mechanical, radiation or thermal energy, among others. Particularly, vibrational energy harvesters transform small mechanical oscillations present in the environment, such as those generated by engines or vehicles, into electrical energy. Although piezoelectric materials are commonly used as active components in this type of harvesters, they show a decrease in efficiency for low-frequency vibrations (<100 Hz), typical of large structures such as bridges or the blades of windmills. In this context, magnetostrictive materials offer superior performance at these frequencies, where the conversion of mechanical to electrical energy is achieved through the Villari effect (variable magnetization and therefore an electromotive force induced in a receiving coil).
However, in order to optimize the converted power density these magnetostrictive vibrational energy harvesters, it is necessary to optimize both the vibrating frame where the magnetostrictive material is fixed, ensuring resonance at the appropriate frequencies, the static magnetic field and the receiving coil responsible for capturing the vibration-induced electric power. Consequently, an optimization problem arises, involving mechanical and electromagnetic aspects.
In this work, we propose the use of the finite element method (FEM) to solve partial differential equations in order to optimize a magnetostrictive vibrational energy harvester. This study focuses on magnetostrictive energy harvesters based on a U-shaped structure [1]. The vibrations generated in the U-shaped structure are transmitted to a magnetostrictive sheet composed of Gallium and Iron (GAFENOL), which is magnetized by permanent magnets (see Fig.1a). The partial differential equations to be addressed will include linear elasticity and Maxwell's equations. The coupling between the mechanical and electromagnetic system is carried out by adjusting the damping coefficients. As an example, Fig.1b shows the estimated electrical power versus frequency, at diferent magnet potitions (x).
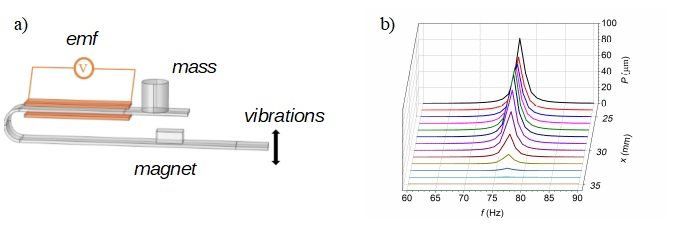
Fig. 1 Optimization of power changing the vibration frequency and magnet position.
Acknowledgements
This work is part of the project TED2021-130884B-I00, founded by “Ministerio de Ciencia e Innovación, Agencia Estatal de Investigación (AEI)” and European Union “Next Generation/PRTR”.
References
[1] T. Ueno, “Magnetostrictive low-cost high-performance vibration power generator,” Journal of Physics: Conference Series, vol. 1052. IOP Publishing, p. 012075, Jul. 2018. doi: 10.1088/1742-6596/1052/1/012075.

