Speaker
Description
Analytical expressions are favored for magnetic field calculations due to their speed compared to finite element simulations [1]. They excel in optimizing high-dimensional systems, allowing efficient exploration of parameter spaces, beneficial for designing cost-effective, robust, and accurate magnetic sensor systems [2]. Despite their usefulness, analytical expressions suffer from the idealized assumption of perfectly homogeneous magnetization. Even in high-quality rare earth magnets, the self-demagnetization effect, arising from the interaction of magnetic moments with the magnet's own field, is a fundamental limitation on the precision of high-precision applications relying on analytical field expressions [3].
We introduce a method using physics-based neural networks (NN) [4] to correct the self-demagnetization error in analytical field expressions. Unlike recent NN approaches [5], we base on the existing analytical solution and train our networks to rectify the errors (see Fig 1), resulting in significantly improved approximations compared to total field calculations with NNs. Our method notably enhances the accuracy of analytical field calculations, particularly in the near field near the magnetic surface, crucial for sensor applications with high amplitudes (see Fig. 2, ascending ordered errors for 1000 different cuboid magnet shapes simulated with assumed remanence polarization of 1T, linear material law and susceptibilities in (0,1), evaluated at different points with amplitudes >25mT). Moreover, the computational time of our NN method remains comparable to analytical expressions, preserving efficient computations even at scale.
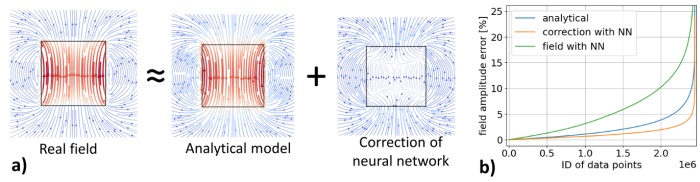
Fig. 1 a) Illustration of our approach: Decomposing the total magnetic field into the analytical model's contribution and a neural network-based correction. b) Comparison of errors: Analytical solution, NN field computation, and our NN-correction to the analytical solution.
Acknowledgements
This work has been supported by Silicon Austria Labs (SAL), owned by the Republic of Austria, the Styrian Business Promotion Agency (SFG), the federal state of Carinthia, the Upper Austrian Research (UAR), and the Austrian Association for the Electric and Electronics Industry (FEEI).
References
[1] M. Ortner and L. G. Coliado Bandeira, “Magpylib: A free Python package for magnetic field computation,” SoftwareX, vol. 11. Elsevier BV, p. 100466, Jan. 2020. doi: 10.1016/j.softx.2020.100466.
[2] M. Ribeiro and M. Ortner, “Magnetic field shaping for improved 1-D linear position measurement,” 2015 9th International Conference on Sensing Technology (ICST). IEEE, Dec. 2015. doi: 10.1109/icsenst.2015.7438486.
[3] D. Cichon, R. Psiuk, H. Brauer, and H. Topfer, “A Hall-Sensor-Based Localization Method With Six Degrees of Freedom Using Unscented Kalman Filter,” IEEE Sensors Journal, vol. 19, no. 7. Institute of Electrical and Electronics Engineers (IEEE), pp. 2509–2516, Apr. 01, 2019. doi: 10.1109/jsen.2018.2887299.
[4] G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang, and L. Yang, “Physics-informed machine learning,” Nature Reviews Physics, vol. 3, no. 6. Springer Science and Business Media LLC, pp. 422–440, May 24, 2021. doi: 10.1038/s42254-021-00314-5.
[5] S. Pollok, N. Olden-Jørgensen, P. S. Jørgensen, and R. Bjørk, “Magnetic field prediction using generative adversarial networks,” Journal of Magnetism and Magnetic Materials, vol. 571. Elsevier BV, p. 170556, Apr. 2023. doi: 10.1016/j.jmmm.2023.170556.

